roshambo, markov chains, and a teaspoon of lulz
30 March 2008As part of his team's “Learn C-Pound” project at the office, KK decided to write a good, old-fashioned rock-paper-scissors server. Bots from around the network would log in and fight one another, 1000 rounds to the death; after several rounds, a winner would be declared.
I suppose there are two ways to get programmers excited to do something: give them a good, useful, open-source tool that they can adapt to their needs (hence the success of the open-source movement); alternately, put them in a code-off, each against the other. The Homestead RPS Tourney definitely appealed to the latter.
The rules were simple: don't directly implement Iocaine Powder, the current world-champion of roshambo. Although a bot using a “always throw random” strategy would be allowed, since everyone would know it was your bot there was a good chance you would receive an IRL beatdown (since a random player not only screws up everyone else's learning algorithms, but also indicates that that must've been your end goal).
an appropriate algorithm
The first big decision about such a program is the method to use to ensure victory. Naïvely, we can come up with some basic strategies:
- Always throw rock
- Throw whatever the opponent threw previously
- Throw whatever would've beaten the opponent's previous throw
- Throw whatever would've lost to the opponent's second-to-last throw
Naturally, there are a potentially-infinite (restricted, in this case, due to the facts that the tourney was only 1000 rounds long and that knowledge is limited to the game state (and random is a specific strategy)) number of strategies to follow here. In some sense, each player could pick some definite strategy such as above, and the tourney would determine which was best suited to beat the others. However, there's not much that's instructive about a bot which always throws rock beating a bot which always throws scissors.
So what can make this competition algorithmically interesting? If the programs are instead designed to learn each others' strategies and beat those — rather than following a fixed set of rules — then the competition becomes about machine learning techniques, and not about rock-paper-scissors. Moreover, any appropriate piece of artificial intelligence should be able to trounce one of the aforementioned fixed strategies (a principle which was brought to bear during th competition).
There are several different methods of looking at this problem, but I chose to look at it as a task in pattern-matching. That is, if we can find that the opponent's behavior follows some known patterns, then we can easily beat it; there is a lot more depth which could be layered onto this method, but any reasonable bot needs to keep a measure of relative behaviors and responses.
We can view the throws of the opponent and ourselves as a series of events, and having seen a specific history we can look at what we've already seen to figure out what we expect to be next. In practice, this is called a Markov chain. The idea is that the next event we see is independent of all events except the immediate precedent:
\[ P(X_{n+1}=x|X_0=x_0, \ldots, X_n=x_n) = P(X_{n+1}=x|X_n=x_n) \]
Now, this idea is probably not the best up-front: in terms of raw events, this means we're restricted to looking at only the previous throw. What if the opponent is following a longer pattern, with more knowledge? Fortunately, we can redefine “event” from a single throw to a tuple of throws. Thus, letting \( T_i \) be the \( i \)th throw, we have:
\[ X_n=(T_n, \ldots, T_{n+k}) \]
For some history length \( k+1 \). With this new definition in order, we have
\[ P(X_{n+1}=x|X_n=x_n) = P(T_{n+k+1}=t_x|T_n=t_n,\ldots,T_{n+k}=t_{n+k}) \]
Where \( t_x \) is the throw in the highest dimension of the history tuple \( x \). Perhaps the best way of visualizing this concept in a CS-friendly manner is to think of a tree:
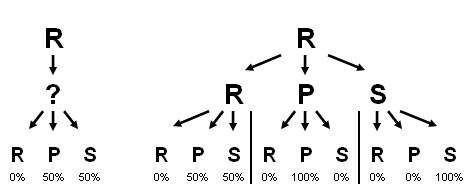 Who needs sgame.sty?
Who needs sgame.sty?In this case, if we know that R was thrown two prior, we're unsure what the next throw will be. However, if we know the previous throw was P, as well, then we fully expect the next throw to be P. Thus we can think of this as a refining tree.
With this ability, we can take any previous event sequence of length \( k+1 \) and make a supposedly-optimal decision of what our subsequent throw should be. Rock on.
making it better
Of course, there are some problems with this method. Besides it susceptibility to randomness (which all learning bots should have as a weakness), there is the distinct possibility that the bot will find itself in unknown territory, given the relative uniqueness of chains past a certain length. To combat this issue, the program maintains chains of multiple depths, each of which votes to determine the overall expected opponent play.
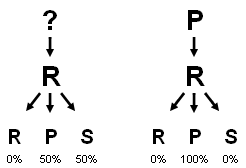 Excel FTW!
Excel FTW!This method, however, suffers its own risks. Let's assume we've just seen PR, and have the history above in mind. The first-level knowledge of merely R will force the bot to choose either P or S; if the bot chooses S, the final vote will be a stalemate and a random choice will ensue. Of course, this is not desireable behavior, since the best next choice is P.
We could solve this problem by having the bot not vote if there's too much indeterminacy in the system, but this solution would require extensive tweaking — never the goal of machine learning (have the system tweak itself!). A simple fix would be to add expected probabilities, but this is arguable: should two 76% certainties be able to override one 100% certainty (in a two-element system)? Possibly, but what if there are ten points of evidence for the 100% certainty, and only five for the 76% certainties? (note that that math doesn't work out in the current context, though it would be possible to construct something similar)
With this in mind, we can construct a certainty function, which provides a weight to apply to the vote from that specific chain length. For \( \tau \) as the number of subsequent instances of R, P, and S in a given chain \( m \), the certainty function \( C \) is:
\[ C(m) = \frac{ \sum_{ t\in \{\mathbf{R},\mathbf{P},\mathbf{S}\}} \tau(m,t)}{\prod_{ t \in\{ \mathbf{R}, \mathbf{P}, \mathbf{S}\}} \left( \tau(m,t) + 1 \right)} \]
Notice that the denominator is largest when the number of subsequent appearances of R, P, and S are similar in magnitude; when one blows the others away, the denominator will be significantly smaller and thus the overall weighting of the vote will be higher.
Since the numerator is equal to the number of times we've seen this history, we see that this function upweights more common histories to normalize their weight — to a certain extent — with less common histories. Thus certainty is truly measured.
With this weighting applied to the empirical probabilities, we have the basis for our comparative metric. Note that this weighting is possibly unnecessary, but performed quite well. In the end, we add up the evident probabilities, multiplied by their respective weights, and select the maximizing throw to be the opponent's next (the one we will beat).
There is some room here for second- and third-guessing logic, but that went reasonably unexplored in this iteration. By and large, this is the algorithm's most significant hole.
implementation
Although it would be possible to have the algorithm measure pure game-state, the probable sparsity of this measurement makes it less than ideal (although it can be used, so long as some adjunct measures are in place). For this reason, two chain histories were constructed: one measuring the opponent's throw in relation to its previous throws, and the other measuring the opponent's throw in relation to our bot's previous throws (of course, a full-state chain could derive these, but it comes to the classic time/space tradeoff).
For each of these chains, we hard-code a maximum history length of 10. I'm a bit hazy on the validity of the logic behind this, but since \( {3}^{10} = 59049 \gg 1000 \) (1000 being the number of rounds per game), coverage of a ten-deep Markov chain should be more than sufficient to uniquely identify most game patterns. (I'm happy to be wrong here; there wasn't that much thought expended and I'm sure my combinatorics are at least a little bit off)
Moreover, the algorithm was implemented in Lolcode — specifically, the YALI dialect (yes, I could've done better than homebrew) — performance on a 10-deep chain was bad enough.
The basic implementation in Lolcode looks as follows:
OBTW
generateThrowVotesFromModel
-----
Given a model and a history, returns the most likely next throw.
TLDR
HOW DUZ I generateThrowVotesFromModel YR markov AN YR history
I HAS A LENF ITZ 10
I HAS A count ITZ 3 IN MAH 0 IN MAH markov UP 3 IN MAH 1 IN MAH markov UP 3 IN MAH 2 IN MAH markov
I HAS A throw
I HAS A votes
LOL 0 IN MAH votes R 0
LOL 1 IN MAH votes R 0
LOL 2 IN MAH votes R 0
I HAS A history_length ITZ ALL history
I HAS A base ITZ history_length NERF LENF
IZ base SMALR THAN 0 ? LOL base R 0
I HAS A _base ITZ base
I HAS A play
I HAS A play_index
I HAS A _markov
I HAS A sum_votes
I HAS A prod_votes
I HAS A weight
I HAS A round_weight
I HAS A weight_base ITZ 1
I HAS A vote_index
I HAS A vote_weight
IM IN YR OUTIE
IZ _base LIEK history_length ? GTFO
LOL base R _base
LOL _markov R markov
LOL round_weight R weight_base BOOMZ ( history_length NERF _base )
IM IN YR INNIE
IZ base LIEK history_length O RLY?
YA RLY
BTW ::: Clearly, need to fix math functions...
LOL sum_votes R 3 IN MAH 0 IN MAH _markov UP 3 IN MAH 1 IN MAH _markov UP 3 IN MAH 2 IN MAH _markov UP 1
LOL prod_votes R 3 IN MAH 0 IN MAH _markov UP 1
LOL prod_votes R prod_votes TIEMZ ( 3 IN MAH 1 IN MAH _markov UP 1 )
LOL prod_votes R prod_votes TIEMZ ( 3 IN MAH 2 IN MAH _markov UP 1 )
LOL weight R sum_votes OVARZ prod_votes
LOL vote_index R 0
IM IN YR LOOP
IZ vote_index LIEK 3 ? GTFO
LOL vote_weight R 3 IN MAH vote_index IN MAH _markov OVARZ sum_votes
LOL vote_weight R vote_weight TIEMZ weight TIEMZ round_weight
LOL vote_index IN MAH votes R vote_index IN MAH votes UP vote_weight
UP vote_index!!
KTHX
GTFO
KTHX
LOL play R base IN MAH history
LOL play_index R getThrowIdByName YR play MKAY
LOL _markov R play_index IN MAH _markov
UP base!!
KTHX
UP _base!!
KTHX
FOUND YR votes
IF U SAY SO
There is an outer function to compile results, and to handle the whole “equal probability” thing. But this is the meat of the chain program.
results
Thing one, I will not be programming in Lolcode again. It was cool for the effort, but now I can officially move on.
In the end, this bot — appropriately named ROFLBOT — was able to demolish some basic bots:
- Always throw rock
- Throw your second-to-last throw
- Throw to beat your last throw
- Throw 30x rock, throw 30x paper, throw 30x scissors...
Fair enough, the algorithm was almost explicitly engineered to handle those cases. Against other learning machines? ROFLBOT fared reasonably well against a variety of other strategies (none of which I remember offhand), and ended up coming in second — a victory for Lolcode users the world 'round. The demolishing bot used a depth of ~500, and was quite willing to throw random if it didn't have knowledge to within a certain threshhold (but honorably so).
Second place. Not bad. Maybe next time.
Go ahead, download ROFLBOT, you know you want to.
Included \(\LaTeX\) graphics are generated at LaTeX to png or by  .
.
contemporary entries
- lessons in python (17 July 2008)
- diy day meets cute overload (10 July 2008)
- roshambo, markov chains, and a teaspoon of lulz (30 March 2008)
- beautiful people (16 March 2008)
- yali: yet another lolcode interpreter (16 March 2008)
view all entries »
comments
Sorry, further commenting on this post has been disabled. For more information, contact me.